Relative Power

Today - something we talked about last week in "class"

Relative power.

In the circuit below -

We have three voltage dividers, in parallel.  R1 and R4 make up the first one.

R2 and R5 are the second, and R3 and R6 the third.

As you can see, the output voltages are 4.21, 12, and 14.19 volts respectively.

How do we calculate the voltages?  With the Voltage Divider Equation:

Where R1 is the bottom resistor, and R2 the top resistor (connected to the power supply)

So in our case, for the first divider we have R1 on top and R4 on the bottom:

So Vout = (1KΩ/(1KΩ+4.7KΩ))*24 volts = 0.1754 * 24 volts = 4.21 volts

We get the other two voltages the same way.

Now how much current is flowing in each divider?

That's easy:  I = E/R, where R in this case is the total series resistance of the divider in question:

So for the first divider, I = 24V/5.7KΩ = 4.21 mA

For the second divider, I = 24V/9.4KΩ = 2.55 mA

For the third divider, I = 24V/11.5KΩ = 2.09 mA

Now for relative power:

Let's look at R1, R2, and R3:

Which one consumes the most power?

That's easy - since R1, R2, and R3 are the same value, and P=I²*R;

The resistor with the most current through it will dissipate the most power.

Since 4.21 mA is the highest current, then R1 will dissipate the most power.

The power dissipated by R1 will be: 4.21mA²*4.7KΩ = 83.30 mW

The power dissipated by R2 will be: 2.55mA²*4.7KΩ = 30.56 mW

Notice that even though the current through R2 is more than half that of R1, that the power dissipated by R2 is less than half that of R1... Why?

Now let's take a look at a simulation from the circuit simulator at http://www.falstad.com/mathphysics.html

scroll down to the "Electrodynamics" section and select 

Analog Circuit Simulator Applet

Here you can build test circuits and see them operate - (on a computer with JAVA installed)

I set the circuit up to show relative power in color - brighter Red means more power:

This agrees well with what we calculated.

I built this circuit in the shop, and I took a thermal picture of it:

And you can see that the thermal picture agrees pretty well with the calculations.

So what do we take from this?

For a given resistor, when the current doubles, the power goes up by four times.

Or... Power is proportional to current squared.

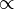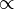P  I²

That's it for now.

Cheers!